Saving for Retirement with Unequal Cash Flows

Published on June 26, 2023 by Eric Liu
Cash Flow Additivity Principle Saving for Retirement
3 min READ
It is likely that people’s saving capacity varies based on different life stages. The ability save may be much smaller in our early career years relative to later years. Uneven cash flows are reasonably expected in our saving plans, such as saving for retirement. When we deal with uneven cash flows, we can take an advantage of cash flow additivity principle – the discounted value of a group of different assets (uneven cash flows) are equivalent to the sum of the discounted value of each individual asset (individual cash flow).
Let us illustrate the dealing of unequal cash flows with an example. Suppose Mark is currently 24 yeas old and wants to retire at age 65. He plans to save $5,000 each year for the next 12 years, and dreams to spend each summer in Europe and ski across the Alps and Rockies every winter when he retires. To afford that, he needs $200,000 per year on average for the next 20 years. Assuming an average return of 9% of his retirement portfolio, how much will Mark need put aside each year for retirement from age 37 to 64?
When it comes to saving for retirement, a timeline helps to visualize the cash flows. Mark is now 24 (t=0) and plans to save $5,000 for the next 12 years. The first cash flow happens when he is 25, and he will save the same amount of money for 12 years until he is 36 (t=12). From age 37 (t=13) to 64 (t=40), he will needs to save a different amount of money each year in order to withdraw $200,000 each year from age 65 (t=41) to age 84 (t=60). We need to figure out how much Mark needs to save from the period of t=41 to t=60.
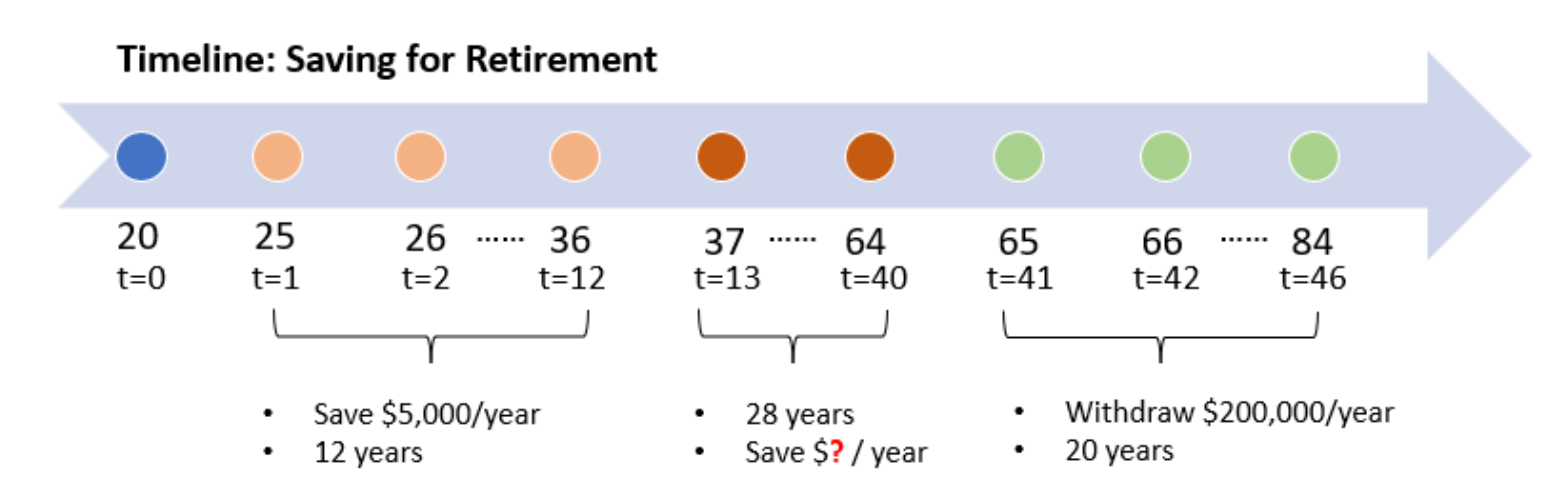
To solve this problem, we can first take a backward look at the retirement period (green from age 65 to 84). Each year, March withdraws $200,000 for 20 years. This looks like an annuity – a series of equal payments made at equal time intervals. We can discount the present value of the annuity back to age 64 as below:
| Notation | Numerical Value |
|---|---|
| PMT | $200,000 |
| N | 20 |
| I/Y | 9% |
| PV* | $1,825,709.13 |
At age 64, to be able to ski in the Alps and spend simmers in Europe, Mark needs to have $1,825,709.13 in order to take out $200,000 for the next 20 years. However, we need to figure out the amount of savings needed for the period from age 37 to 64 (red). The present value of the annuity at age 64 is the tantamount to the future value of the savings at age 36. How much savings does Mark need to have at age 36 to achieve his retirement goal? We can discount the amount of $1,825,709.13 back for 28 periods.
| Notation | Numerical Value |
|---|---|
| FN | $1,825,709.13 |
| N | 28 |
| I/Y | 9% |
| PV* | $163,489.42 |
At age 36, Mark needs to have $163,489.42. How much will Mark actually have if he saves at the rate of $5,000 per year for 12 years?
| Notation | Numerical Value |
|---|---|
| PMT | $5,000 |
| N | 12 |
| I/Y | 9% |
| PV* | $100,703.60 |
Mark will have $100,703.60 at age 36 if he saves $5,000 for 12 years at 9% discount rate. However, to achieve his retirement goal, he needs to have $163,489.42. Based on the cash flow additivity principle, the discounted value of a group of different cash flows is equal to the sum of each individual discounted value of cash flow. $163,489.42 is the present value of the retirement goal at age 37. $100,703.60 is the future value of the past savings at age 37. The difference ($62,785.82) between these two amounts is the present value of the annuity payments from age 37 to 64.
| Notation | Numerical Value |
|---|---|
| PV | $62,785.82 |
| N | 28 |
| I/Y | 9% |
| PMT* | $6,206.51 |
Mark needs to increase his savings from $5,000 per year to $6,206.51 per year from age 37 to 64 in order to meet his retirement goal.